
Zadanie Krążki (kra)
Pomóż nam usprawnić bazę zadań!
Krążki
Limit pamięci: 32 MB
Mały Jaś dostał od rodziców na urodziny nową zabawkę, w której skład wchodzą rurka i krążki. Rurka ma nietypowy kształt - mianowicie jest to połączenie pewnej liczby walców (o takiej samej grubości) z wyciętymi w środku (współosiowo) okrągłymi otworami różnej średnicy. Rurka jest zamknięta od dołu, a otwarta od góry. Na poniższym rysunku przedstawiono przykładową taką rurkę, złożoną z walców, w których wycięto otwory o średnicach kolejno: 5 cm, 6 cm, 4 cm, 3 cm, 6 cm, 2 cm i 3 cm.
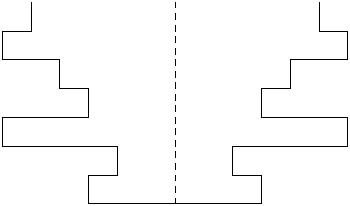
Krążki w zabawce Jasia są walcami o różnych średnicach i takiej samej grubości co walce tworzące rurkę.
Jaś wymyślił sobie następującą zabawę. Mając do dyspozycji pewien zestaw krążków zastanawia się, na jakiej wysokości zatrzymałby się ostatni z nich, gdyby wrzucał je kolejno do rurki centralnie (czyli dokładnie w jej środek). Dla przykładu, gdyby wrzucić do powyższej rurki krążki o średnicach kolejno 3 cm, 2 cm i 5 cm, to otrzymalibyśmy następującą sytuację:
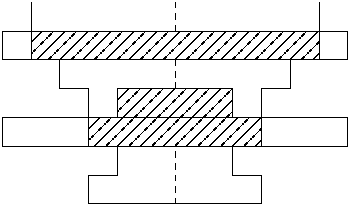
Jak widać, każdy kolejny krążek po wrzuceniu spada dopóki się nie zaklinuje (czyli nie oprze się o walec, w którym wycięty jest otwór o mniejszej średnicy niż średnica krążka), albo nie natrafi na przeszkodę w postaci innego krążka lub dna rurki.
Ponieważ zabawa ta jest trudna dla małego Jasia, to ciągle prosi swoich rodziców o pomoc. A jako że rodzice Jasia nie lubią takich zabaw intelektualnych, to poprosili Ciebie - znajomego programistę - o napisanie programu, który zamiast nich będzie udzielał odpowiedzi Jasiowi.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia schemat rurki i opis krążków jakie Jaś będzie wrzucał do rurki,
- wyznaczy głębokość, na jakiej zatrzyma się ostatni wrzucony przez Jasia krążek,
- wypisze wynik na standardowe wyjście.
Wejście
Pierwszy wiersz wejścia zawiera dwie liczby całkowite  i
i 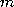 (
(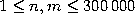 ), oddzielone pojedynczym odstępem
i oznaczające wysokość rurki Jasia (liczbę walców wchodzących
w jej skład) i liczbę krążków, które zamierza wrzucić do rurki.
Drugi wiersz wejścia zawiera
), oddzielone pojedynczym odstępem
i oznaczające wysokość rurki Jasia (liczbę walców wchodzących
w jej skład) i liczbę krążków, które zamierza wrzucić do rurki.
Drugi wiersz wejścia zawiera  liczb całkowitych
liczb całkowitych  (
(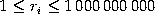 dla
dla 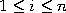 )
oddzielonych pojedynczymi odstępami
i oznaczających średnice otworów wyciętych w kolejnych (od góry)
walcach tworzących rurkę.
Trzeci wiersz wejścia zawiera
)
oddzielonych pojedynczymi odstępami
i oznaczających średnice otworów wyciętych w kolejnych (od góry)
walcach tworzących rurkę.
Trzeci wiersz wejścia zawiera 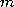 liczb całkowitych
liczb całkowitych
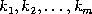 (
(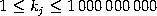 dla
dla 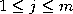 )
oddzielonych pojedynczymi odstępami
i oznaczających średnice kolejnych krążków, które Jaś zamierza
wrzucić do rurki.
)
oddzielonych pojedynczymi odstępami
i oznaczających średnice kolejnych krążków, które Jaś zamierza
wrzucić do rurki.
Wyjście
Pierwszy i jedyny wiersz wyjścia powinien zawierać jedną liczbę całkowitą, oznaczającą głębokość zatrzymania się ostatniego krążka. Jeżeli krążek ten w ogóle nie wpadnie do rurki, to odpowiedzią powinna być liczba 0.
Przykład
Dla danych wejściowych:
7 3 5 6 4 3 6 2 3 3 2 5
poprawną odpowiedzią jest:
2
Autor zadania: Jakub Radoszewski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English